CoffeeNews.it Edilizia e Fai da te
Geometria formule figure piane e solidi, ben si addice a coloro che operano nel ramo edile e che spesso, magari per motivi di contabilità dei lavori, hanno a che fare con superfici piane più o meno complesse o con solidi di forma varia.
Ricordarsi le relative formule non è sempre possibile; per cui con questo articolo vogliamo aiutare tutti quelli che ne avranno necessità.
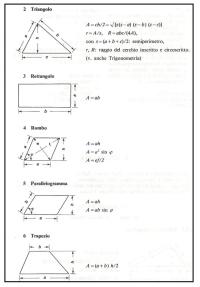
1) Le figure piane
Il triangolo rettangolo è sicuramente la figura piana più semplice e si può facilmente calcolare sia la sua superficie che il suo volume.
Di seguito, a sinistra, riportiamo la tabella n° 2 riferita ad un triangolo qualunque, ad un rettangolo, rombo, parallelogramma e trapezio.
Di fianco alla tabella due si trova la tabella 3 che riporta le immagini e le relative formule di sviluppo delle seguenti figure geometriche: quadrilatero, poligono regolare, poligono generico, cerchio, corona circolare
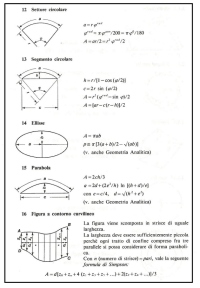
Proseguiamo con le figure piane, rappresentando: il settore circolare, il segmento circolare, l’elisse, la parabola ed infine una figura a contorno curvilineo da scomporre in strisce di uguale larghezza.
Relativamente a questa ultima figura proseguiamo la formula con una tabellina aggiuntiva, a completamento della precedente
2) I Solidi
E’ importante riuscire a risolvere i vari volumi che si possono trovare nell’ambito di una costruzione, e che non sono sempre regolari.
Di seguito riportiamo le tabelle significative riferite ai solidi facili ed a quelli di più difficile risoluzione.
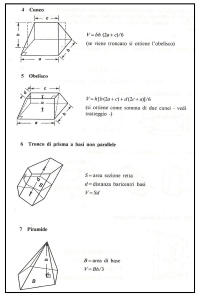
Sicuramente il parallelepipedo è la forma volumetrica o solido più comune, e non si presterà a difficoltà di calcolo, ma seguono altre, più difficili, quali: il prisma con basi parallele retto e oblique e poi il tronco di prisma triangolare.
Nella seconda tabella soprastante e rappresentata a destra abbiamo invece il cuneo, l’obelisco il tronco di prisma a basi non parallele e la piramide: figure più complesse e per le quali troverete sicuramente un valido aiuto.
Proseguiamo rappresentando altre due tabelle dedicate alle figure dei solidi ed alle loro rispettive formule risolutive.
Nella tabella a sinistra abbiamo: la piramide retta a base regolare, il tronco di piramide a basi parallele, il prismoide ed infine le rampe.
Quest’ultimo è sicuramente un solido che ricorrerà spesso nelle contabilità di cantiere e vi permetterà di prendere le misure necessarie al suo calcolo
Nella soprastante immagine a destra sono rappresentati i solidi complessi riferiti a: cilindro circolare retto e obliquo, tronco di cilindro circolare, cono circolare retto ed obliquo, tronco di cono circolare a basi parallele.
Per completare questa nostra passeggiata fra le figure geometriche, riportiamo sopra le due tabelle finali.
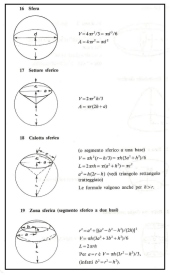
La tabella di sinistra riferita a: sfera, settore sferico, calotta sferica, zona sferica (Segmento sferico a due basi)
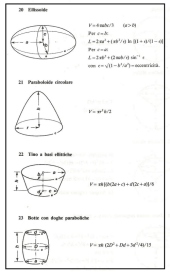
La tabella di destra riferita a: elissoide, paraboloide circolare, tino a basi ellittiche, botte con doghe paraboliche.
Siamo consci che non tutte le figure geometriche che vi abbiamo mostrato in questo nostro articolo vi potranno servire in futuro; comunque abbiamo preferito presentarvi un quadro completo delle stesse.
